


Tytuł
NA GAPĘAutor
Sławomir DziugiełDział
Gra dla całej klasyInnowacyjne cele edukacyjne
Powszechnie wiadomo, że dziecko wolałoby pobawić się z kolegami niż uczestniczyć w zajęciach z matematyki. Dlatego warto połączyć te dwie kwestie, aby zainteresować dzieci lekcją i omawianymi na niej zagadnieniami.
Nauka poprzez zabawę jest najefektywniejszym sposobem zdobywania wiedzy przez dzieci i młodzież. Ważne jest tylko, aby we właściwy sposób przekazać w grze odpowiednie treści oraz dobrać je do wieku i poziomu uczniów, jak również uwzględnić możliwości techniczne przeprowadzenia takiej lekcji.
Biorąc pod uwagę wszystkie wspomniane powyżej kwestie stworzyliśmy zbiór uniwersalnych gier o nazwie „Gry Dziuglaka”. Oznacza to, że używając schematu gier można je wykorzystywać do omawiania różnych zagadnień matematycznych i o różnym stopniu trudności w zależności od poziomu uczniów i potrzeb nauczyciela. Poprzez uniwersalność naszych gier rozumiemy również możliwość wykorzystania ich za pomocą różnych środków dostępu i przekazu, tzn. gry mogą być przeprowadzane przy pomocy komputera, multimediów jak również korzystając z tradycyjnych form tj. gier planszowych czy zabaw grupowych. Formuła gier przewiduje możliwość wzięcia udziału w grze indywidualnie, gdzie każdy uczestnik musi polegać jedynie na sobie, jak również gry te można przełożyć na pracę w grupach, gdzie można liczyć na pomoc i wsparcie ze strony kolegów ze swojej drużyny. Pozytywnym aspektem gier grupowych jest rodząca się z ich struktury chęć rywalizacji między uczestnikami, co stanowi motywator do pracy i pogłębiania swojej wiedzy oraz zdobywania nowych umiejętności. Należy pamiętać, że każdą grę nauczyciel może dostosować do swoich warunków. „Gry Dziuglaka” doskonale sprawdzają się jako powtórzenie po omówionym dziale, które pomoże uczniom poprzez zabawę utrwalić zdobytą na zajęciach wiedzę.
Oczywiście utrwalenie określonych wiadomości nie jest jedyną funkcją gier. Oprócz tego ich głównym celem jest rozwijanie zdolności matematycznych uczniów, wspomaganie logicznego, strategicznego i kreatywnego myślenia. Poprzez grę każdy uczeń jest zaangażowany w wykonywane zadania i bierze w nich aktywny udział, co sprawi, że zajęcia stają się atrakcyjne dla każdego.
Czas
dowolnyPrzebieg
OGÓLNE ZASADY GRY
Gracze są roztargnionymi matematykami, jadącymi na międzynarodowy kongres młodych uczonych. Tym wydarzeniem są tak przejęci, że wsiadają do pociągu bez biletów. Niestety, okazuje się, że nie mogą znaleźć też portfeli. Muszą więc podróżować na gapę, gdyż nigdy w życiu nie darowaliby sobie opuszczenia tego nadzwyczajnego spotkania. Szybko wymyślają, że aby nie dać się złapać konduktorowi, będą na każdej stacji przechodzić do innego wagonu. A jeśli ten sposób by zawiódł, spróbują konduktorowi wytłumaczyć całą sytuację i udowodnić, że kongres dużo by stracił pod ich nieobecność. Gracze mają jednak szczęście, gdyż konduktor okazuje się zamiłowanym matematykiem-amatorem i jest w stanie przymknąć oko na pasażera jadącego na gapę, jeśli ten pokaże mu ciekawe zadanie.
WIZAUALIZACJA GRY
- Rysunek pociągu z dziesięcioma wagonami jadącego po osi liczbowej. Numery wagonów powinny odpowiadać skali osi.
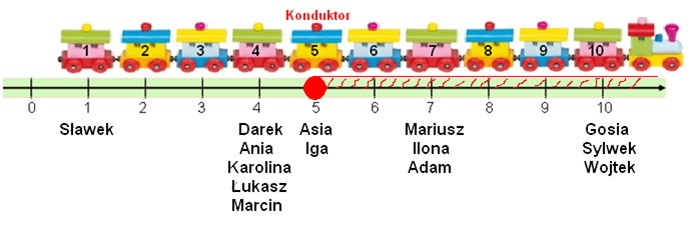
- Na każdej stacji zaznaczamy, w którym wagonie znajduje się konduktor i w którą stronę pociągu będzie szedł, sprawdzając bilety. Również zaznaczamy te informacje na osi liczbowej w postaci przedziału oraz zapisujemy pod wagonem nazwiska graczy, którzy się w nim znajdują.
PRZEBIEG GRY
- Gra dzieli się na dziesięć stacji. Na każdej stacji gracz wybiera dla siebie wagon, wsiada do niego i kiedy pociąg rusza, rozwiązuje zadanie, którym będzie mógł zainteresować konduktora i uniknąć kary za jazdę bez biletu.
- Dalej losujemy wagon, do którego wchodzi konduktor, oraz jeden ze znaków nierówności słabej bądź ostrej.
- Na przykład
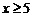 (tak jak pokazano na rysunku) oznacza, że konduktor wszedł do wagonu nr 5 i zacznie sprawdzać bilety wszystkim pasażerom, począwszy od tego wagonu w stronę czoła pociągu, czyli Asi, Idze, Mariuszowi, Ilonie, Adamowi, Gosi, Sylwkowi i Wojtkowi. Zapis x>5 oznaczałby, że konduktor wszedł również do wagonu nr 5, ale zacząłby sprawdzać bilety od wagonu następnego, idąc w stronę tyłu pociągu, czyli Darkowi, Ani, Karolinie, Łukaszowi, Marcinowi oraz Sławkowi.
(tak jak pokazano na rysunku) oznacza, że konduktor wszedł do wagonu nr 5 i zacznie sprawdzać bilety wszystkim pasażerom, począwszy od tego wagonu w stronę czoła pociągu, czyli Asi, Idze, Mariuszowi, Ilonie, Adamowi, Gosi, Sylwkowi i Wojtkowi. Zapis x>5 oznaczałby, że konduktor wszedł również do wagonu nr 5, ale zacząłby sprawdzać bilety od wagonu następnego, idąc w stronę tyłu pociągu, czyli Darkowi, Ani, Karolinie, Łukaszowi, Marcinowi oraz Sławkowi.
- Każdy sprawdzany między stacjami gracz, jeśli ma dobrze rozwiązane zadanie, unika kary łaskawego konduktora. Jeśli zadania nie rozwiązał poprawnie, otrzymuje karę – minus jeden punkt.
ZWYCIĘSTWO W GRZE
- Po dojeździe do celu podróży, do stacji dziesiątej, wyłaniamy zwycięskiego gracza. Zostaje nim ten, kto ma najmniej punktów ujemnych.
- W razie równej liczby punktów ujemnych, bądź zera (jeśli nie popełnił żadnego błędu w zadaniach bądź skutecznie unikał kontroli) wygrywa ten gracz, który ma najmniej razy kasowany bilet, czyli rzadziej był kontrolowany.
Podsumowanie
WSKAZÓWKI DLA NAUCZYCIELA
- Zaleca się wprowadzenia tej gry po zrealizowaniu działu liczby wymierne dla utrwalenie liczb ujemnych oraz umiejętności zaznaczania przedziałów na osi liczbowej. Uczniowie powinni sami zaznaczać przedział wymagany do rozegrania każdej części (stacji) gry, a nazwy stacji powinny jednoznacznie odzwierciedlać wiedzę wymaganą do rozwiązania zadania.
- Proponowane nazwy stacji (części gry):
1. Porównywanie
2. Dodawanie
3. Odejmowanie
4. Mnożenie
5. Dzielenie
6. Kolejność wykonywania działań
7. Potęgi
8. Pierwiastki
9. Zadania tekstowe
10. Liczby niewymierne
11. Zaokrąglanie
12. Kalkulator
Liczba stacji (części gry) może być dowolna.


