


Tytuł
OKRĄGLAKAutor
Sławomir DziugiełDział
Gra dla całej klasy (min. 8 osób)Innowacyjne cele edukacyjne
Powszechnie wiadomo, że dziecko wolałoby pobawić się z kolegami niż uczestniczyć w zajęciach z matematyki. Dlatego warto połączyć te dwie kwestie, aby zainteresować dzieci lekcją i omawianymi na niej zagadnieniami.
Nauka poprzez zabawę jest najefektywniejszym sposobem zdobywania wiedzy przez dzieci i młodzież. Ważne jest tylko, aby we właściwy sposób przekazać w grze odpowiednie treści oraz dobrać je do wieku i poziomu uczniów, jak również uwzględnić możliwości techniczne przeprowadzenia takiej lekcji.
Biorąc pod uwagę wszystkie wspomniane powyżej kwestie stworzyliśmy zbiór uniwersalnych gier o nazwie „Gry Dziuglaka”. Oznacza to, że używając schematu gier można je wykorzystywać do omawiania różnych zagadnień matematycznych i o różnym stopniu trudności w zależności od poziomu uczniów i potrzeb nauczyciela. Poprzez uniwersalność naszych gier rozumiemy również możliwość wykorzystania ich za pomocą różnych środków dostępu i przekazu, tzn. gry mogą być przeprowadzane przy pomocy komputera, multimediów jak również korzystając z tradycyjnych form tj. gier planszowych czy zabaw grupowych. Formuła gier przewiduje możliwość wzięcia udziału w grze indywidualnie, gdzie każdy uczestnik musi polegać jedynie na sobie, jak również gry te można przełożyć na pracę w grupach, gdzie można liczyć na pomoc i wsparcie ze strony kolegów ze swojej drużyny. Pozytywnym aspektem gier grupowych jest rodząca się z ich struktury chęć rywalizacji między uczestnikami, co stanowi motywator do pracy i pogłębiania swojej wiedzy oraz zdobywania nowych umiejętności. Należy pamiętać, że każdą grę nauczyciel może dostosować do swoich warunków. „Gry Dziuglaka” doskonale sprawdzają się jako powtórzenie po omówionym dziale, które pomoże uczniom poprzez zabawę utrwalić zdobytą na zajęciach wiedzę.
Oczywiście utrwalenie określonych wiadomości nie jest jedyną funkcją gier. Oprócz tego ich głównym celem jest rozwijanie zdolności matematycznych uczniów, wspomaganie logicznego, strategicznego i kreatywnego myślenia. Poprzez grę każdy uczeń jest zaangażowany w wykonywane zadania i bierze w nich aktywny udział, co sprawi, że zajęcia stają się atrakcyjne dla każdego.
Czas
dowolnyPrzebieg
OGÓLNE ZASADY GRY
Każdy z graczy ma za zadanie dotrzeć do okrąglaka, czyli do centralnego okręgu.
WIZAUALIZACJA GRY
Okręgi, w takim układzie jak na rysunku, można wyznaczać za pomocą szarf bądź sznurków tak jak pokazano na rysunku.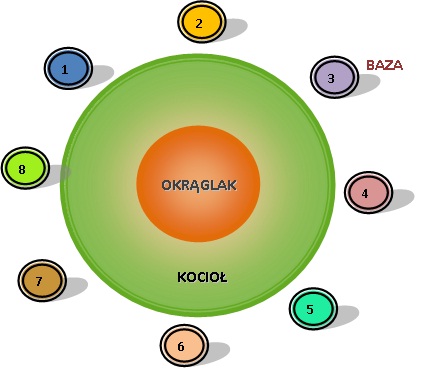
PRZEBIEG GRY
- Po przygotowaniu placu gry jak pokazano na rysunku, gracze losują po jednym zadaniu i stają w dowolnej bazie. Wśród tych zadań jest jedno, które ma specjalny znacznik. Oznacza to, że posiadacz tego zadania jest strażnikiem. O tym wie tylko on sam.
- Gracze, po zajęciu bazy, mają ściśle określony czas na rozwiązanie zadania. Po upływie tego czasu, ujawnia się strażnik. Wydaje jedno z dwu poleceń: baza bądź kocioł. W późniejszej fazy gry dojdzie jeszcze jedno polecenie: okrąglak!
- Jeśli na początku gry pada hasło baza, nic się nie dzieje. Każdy zostaje na swoim miejscu. Jeśli pada hasło kocioł, gracze, którzy stwierdzą, że rozwiązali prawidłowo zadanie, mogę wyjść z bazy i skierować się w stronę centralnego okręgu, znaleźć się w kotle, tuż przy okrąglaku!
- W kotle następuje weryfikacja zadań graczy. W bazie zadania nie są sprawdzane. Jeśli zadanie jest rozwiązane poprawnie, gracz zostaje w kotle. Jeśli popełnił błąd, jest wycofywany na zewnątrz od swojej bazy, staje się wygnańcem.
- Następuje ciąg dalszy gry. Uczestnicy losują nowe zadanie, w tym jedno ze znacznikiem. Mamy nowego strażnika.
- Znowu odmierzamy czas na rozwiązanie zadania, a po jego upływie ujawnia się strażnik. Jeśli powie baza, wszyscy gracze znowu zajmują miejsce na obrzeżach gry. Wycofują się nawet ci, którzy byli już w kotle. Mają prawo też zająć miejsce w bazie wygnańcy. Dalej nic się nie dzieje. Wszyscy uczestnicy znajdują się w bazie. Zadanie nie jest sprawdzane. Jeśli strażnik zdecyduje się powiedzieć kocioł, to ci gracze wchodzą do kotła bądź w nim zostają, którym udało się prawidłowo rozwiązać zadanie. Teraz sprawdzane są zadania z konsekwencjami jak było na początku gry.
- Znowu sytuacja się powtarza. Są losowane nowe zadania. Będzie też nowy strażnik. Gra się kończy w momencie, aż jakiś strażnik powie okrąglak, Może to wypowiedzieć, jeśli rozwiązał prawidłowo zadanie i znajdował się w kotle. Po wypowiedzeniu tego hasła, strażnik wchodzi do okrąglaka, a za nim wszyscy inni gracze, którzy tak jak on stali w kotle i dobrze rozwiązali zadanie. Po tym następuje sprawdzenie zadań w okrąglaku. Ci, którzy dobrze rozwiązali zadania – są zwycięzcami. Po poleceniu okrąglak nie mają prawa ruchu gracze zajmujący bazę. Nie mogą oni wejść do kotła nawet, jeśli uważają, że mają dobrze rozwiązane zadanie. Gdyby okazało się, że wszyscy gracze, którzy weszli do okrąglaka, mają źle rozwiązane zadania, stają się oni wygnańcami i gra toczy się dalej.
ZWYCIĘSTWO W GRZE
Wejście do centralnego okręgu – okrąglaka zapewnia tylko strażnik, który w poprzednim ruchu znajdował się w kotle. Poza tym swoje zwycięstwo po wejściu do okrąglaka musi potwierdzić prawidłowo rozwiązanym zadaniem. W innym przypadku staje się wygnańcem. Tak więc grę można wygrać samemu, będąc tylko strażnikiem albo być jednym ze współzwycięzców, czyli w momencie wypowiedzenia hasła okrąglak, znajdować się w kotle i mieć dobrze rozwiązane zadanie.
Podsumowanie
WSKAZÓWKI DLA NAUCZYCIELA
Ta gra sprawdza się wyśmienicie przy dobrej pogodzie na świeżym powietrzu. Wtedy potrzeba tylko trochę placu czy boiska. Uczniowie wtedy powinni zaopatrzyć się w coś do pisania oraz twarde podkładki. Gracze podczas jednego ruchu mogą rozwiązywać to samo zadanie.

