


Tytuł
PARKUR MATEMATYCZNYAutor
Sławomir DziugiełDział
Gra zespołowaInnowacyjne cele edukacyjne
Powszechnie wiadomo, że dziecko wolałoby pobawić się z kolegami niż uczestniczyć w zajęciach z matematyki. Dlatego warto połączyć te dwie kwestie, aby zainteresować dzieci lekcją i omawianymi na niej zagadnieniami.
Nauka poprzez zabawę jest najefektywniejszym sposobem zdobywania wiedzy przez dzieci i młodzież. Ważne jest tylko, aby we właściwy sposób przekazać w grze odpowiednie treści oraz dobrać je do wieku i poziomu uczniów, jak również uwzględnić możliwości techniczne przeprowadzenia takiej lekcji.
Biorąc pod uwagę wszystkie wspomniane powyżej kwestie stworzyliśmy zbiór uniwersalnych gier o nazwie „Gry Dziuglaka”. Oznacza to, że używając schematu gier można je wykorzystywać do omawiania różnych zagadnień matematycznych i o różnym stopniu trudności w zależności od poziomu uczniów i potrzeb nauczyciela. Poprzez uniwersalność naszych gier rozumiemy również możliwość wykorzystania ich za pomocą różnych środków dostępu i przekazu, tzn. gry mogą być przeprowadzane przy pomocy komputera, multimediów jak również korzystając z tradycyjnych form tj. gier planszowych czy zabaw grupowych. Formuła gier przewiduje możliwość wzięcia udziału w grze indywidualnie, gdzie każdy uczestnik musi polegać jedynie na sobie, jak również gry te można przełożyć na pracę w grupach, gdzie można liczyć na pomoc i wsparcie ze strony kolegów ze swojej drużyny. Pozytywnym aspektem gier grupowych jest rodząca się z ich struktury chęć rywalizacji między uczestnikami, co stanowi motywator do pracy i pogłębiania swojej wiedzy oraz zdobywania nowych umiejętności. Należy pamiętać, że każdą grę nauczyciel może dostosować do swoich warunków. „Gry Dziuglaka” doskonale sprawdzają się jako powtórzenie po omówionym dziale, które pomoże uczniom poprzez zabawę utrwalić zdobytą na zajęciach wiedzę.
Oczywiście utrwalenie określonych wiadomości nie jest jedyną funkcją gier. Oprócz tego ich głównym celem jest rozwijanie zdolności matematycznych uczniów, wspomaganie logicznego, strategicznego i kreatywnego myślenia. Poprzez grę każdy uczeń jest zaangażowany w wykonywane zadania i bierze w nich aktywny udział, co sprawi, że zajęcia stają się atrakcyjne dla każdego.
Czas
dowolnyPrzebieg
OGÓLNE ZASADY GRY
Parkur to ogrodzony plac z przeszkodami, które pokonuje jeździec na koniu. Gracz wciela się w postać takiego jeźdźca i punktuje dla swojej drużyny-stajni na jednej przeszkodzie, z tym że przeszkody pokonuje się zadaniami matematycznymi.
WIZUALIZACJA GRY
Tabela wyników pokonywania kolejnych przeszkód oraz ewentualnie rycina parkura (oddająca jedynie ducha gry).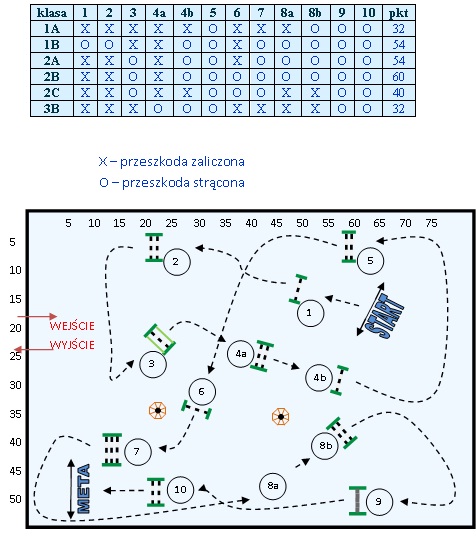
PRZEBIEG GRY
- Każda drużyna-stajnia rozstawia swoich zawodników do poszczególnych przeszkód. Jest to o tyle ważne, że za zaliczenie przeszkód przyznawana jest różna liczba punktów.
- Numer przeszkody oznacza jednocześnie liczbę punktów za jej pokonanie. Nie ma wpływu na punktację to, że przeszkoda ma numer np. 4a. Na tej przeszkodzie można zdobyć 4 pkt.
- Następnie przystępujemy do zasadniczej fazy gry – pokonania przeszkody. W tym celu każdy gracz drogą losową otrzymuje zadanie i przystępuje samodzielnie do jego rozwiązywania. Jeśli rozwiąże je prawidłowo, to oznacza, że przeszkodę zaliczył i wtedy zyskuje dla swojej drużyny liczbę punktów równą numerowi pokonanej przeszkody. Popełniając błąd w rozwiązaniu, strąca przeszkodę i nie zdobywa punktów dla drużyny.
ZWYCIĘSTWO W GRZE
- Po podejściach do wszystkich przeszkód na parkurze, drużyny-stajnie porównują swój dorobek.
- Wygrywa ta drużyna, która zebrała największą liczbę punktów. W przypadku równej liczby punktów kilku drużyn, za zwycięską uznaje się tę, której gracze pokonali więcej przeszkód.
Podsumowanie
WSKAZÓWKI DLA NAUCZYCIELA
- Najlepiej grę stosować do porównywania poziomu przyswojenia bieżących tematów między uczniami. Wtedy gra jest korespondencyjna. W przypadku większej liczby uczniów niż przeszkód, czyli niż 12 osób, dozwolone jest wprowadzanie kolejnych przeszkód, jak to pokazano w tej wersji gry z przeszkodami nr 4 i nr 8 albo przydzielenie dwóch zawodników do tej samej przeszkody. Wówczas drużyna zdobywa punkty za tę przeszkodę, jeśli przynajmniej jeden z graczy ją pokonał. Nie można oczywiście przyznać podwójnej liczby punktów w przypadku, gdyby ci dwaj gracze prawidłowo rozwiązali zadania.
- Zastosować można też wariant indywidualny tej gry. Wtedy każdy zawodnik ma do pokonania wszystkie przeszkody i rozwiązuje wszystkie potrzebne do tego zadania. Prowadzi się wtedy klasyfikację indywidualne. Wskazane jest też odnotowywanie rekordów życiowych ucznia.

