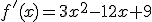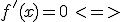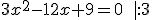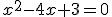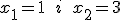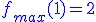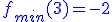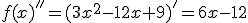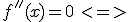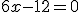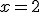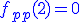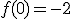Przebieg zmienności funkcji - monotoniczność, ekstrema, punkty przegięcia
Autor
Dariusz KulmaWstępBadanie przebiegu zmienności funkcji, a w szczególności określenie monotoniczności i znajdowanie wartości ekstremalnych oraz punktów przegięcia to obszar matematyki, w którym szczególne zastosowanie ma rachunek pochodnych. Spróbujmy na przykładzie omówić te pojęcia. |
 |
PrzykładZbadaj przebieg zmienności funkcji |
1. Obliczamy pierwszą pochodną funkcji
2. Przyrównujemy pierwszą pochodną do zera.
czyli:
|
3. Rysujemy szkic pochodnejPo narysowaniu szkicu pochodnej, która w tym przypadku jest parabolą, określamy, gdzie pochodna jest dodatnia, a gdzie ujemna. |
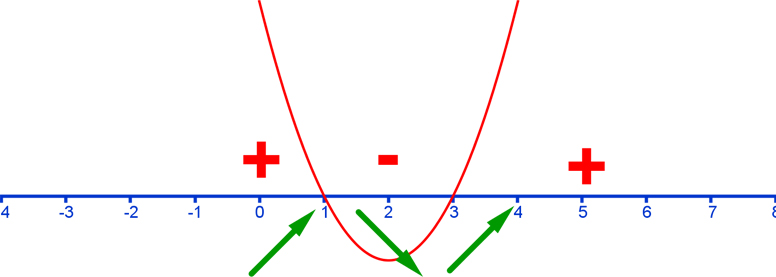 |
4. Własności wynikające z pierwszej pochodnejZgodnie z twierdzeniem - jeśli pochodna ma miejsca zerowe, to znaczy, że funkcja może mieć wartosci ekstremalne dla tych właśnie miejsc zerowych. W tym przypadku funkcja może mieć dwa ekstrema lokalne dla x=1 i dla x=3. Jeśli pochodna ma wartość dodatnią w określonym przedziale, to znaczy, że funkcja jest w tym przedziale rosnąca, a jeśli ma wartość ujemną w określonym przedziale, to funkcja w tym przedziale jest malejąca.
Jeśli funkcja jest przed miejscem zerowym rosnąca, a potem malejąca to znaczy, że w miejscu zerowym pochodnej znajduje sie MAKSIMUM czyli:
Jeśli funkcja jest przed miejscem zerowym malejąca, a potem rosnąca, to znaczy, że w miejscu zerowym pochodnej znajduje się MINIMUM czyli:
|
5. Obliczamy drugą pochodnąDrugą pochodną otrzymamy, jeśli obliczymy pochodną z pierwszej pochodnej
6. Przyrównujemy drugą pochodną do zera
czyli:
|
7. Rysujemy szkic drugiej pochodnejPo narysowaniu szkicu drugiej pochodnej, która w tym przypadku jest funkcją liniową, określamy, gdzie pochodna jest dodatnia, a gdzie ujemna. |
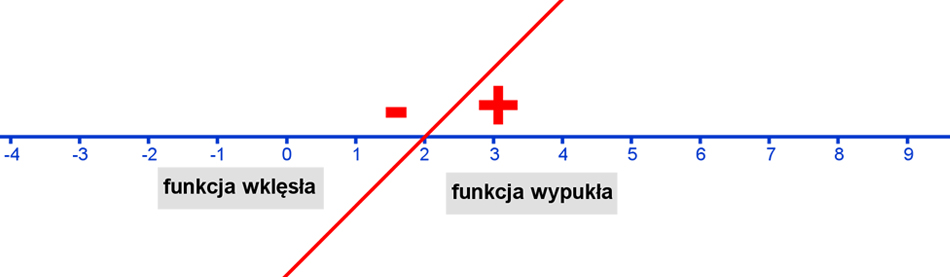 |
9. Własności wynikające z drugiej pochodnejZgodnie z twierdzeniem - jeśli druga pochodna ma miejsca zerowe, to znaczy, że funkcja może mieć punkty przegięcia dla tych właśnie miejsc zerowych. W tym przypadku dla x=2 funkcja może mieć punkt przegięcia czyli:
Jeśli druga pochodna ma wartość dodatnią w określonym przedziale, to znaczy, że funkcja jest w tym przedziale wypukła, a jeśli ma wartość ujemną w określonym przedziale, to funkcja w tym przedziale jest wklęsła. |
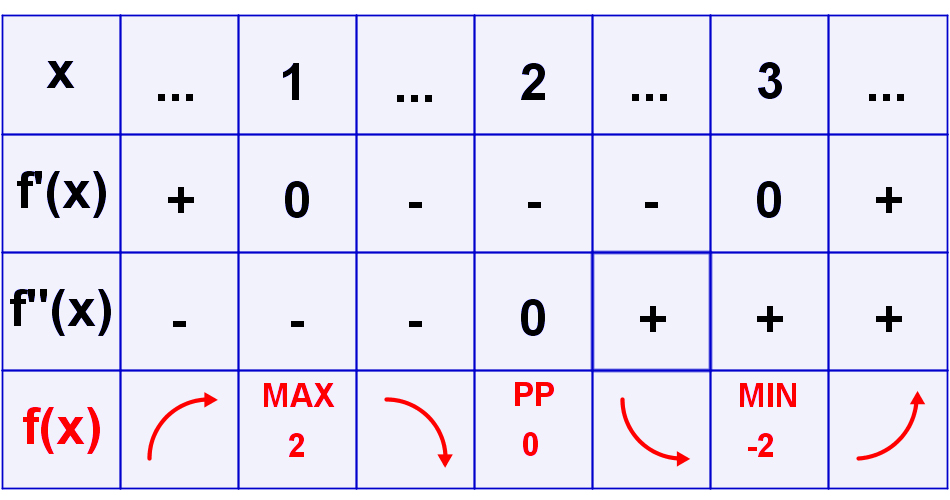
10. Zebranie informacji o funkcji w tabeliUzupełniamy tabelę na podstawie szkiców pierwszej i drugiej pochodnej. Strzałka skierowana w górę oznacza funkcję rosnącą, strzałka w dół - funkcję malejącą. Wygięcie strzałki w odpowiednią stronę opisuje czy funkcja jest wklęsła czy wypukła. |
 |
11. Wykonanie rysunku funkcjiNajpierw liczymy przecięcie z osią OY.
|
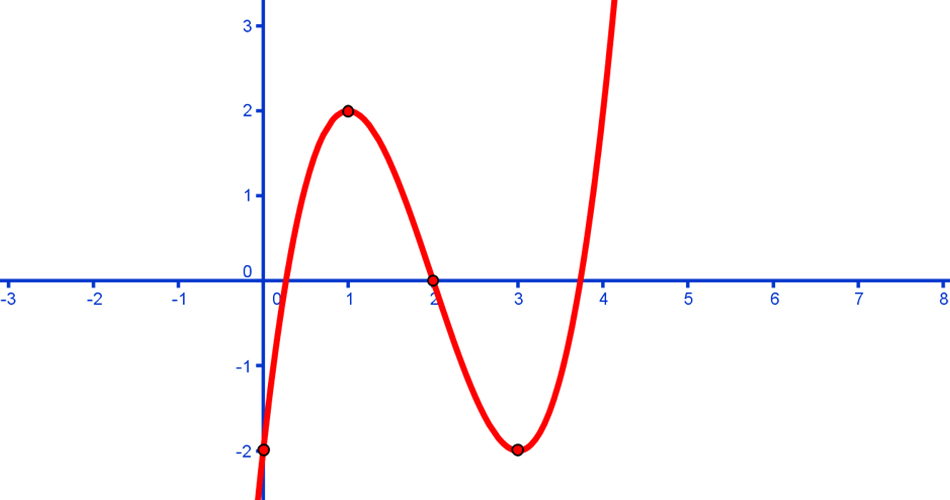 |


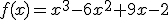 określając monotoniczność, ekstrema i punkty przegięcia. Sporządź wykres tej funkcji.
określając monotoniczność, ekstrema i punkty przegięcia. Sporządź wykres tej funkcji.