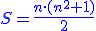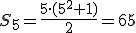Kwadraty magiczne
Autor
Dariusz Kulma |
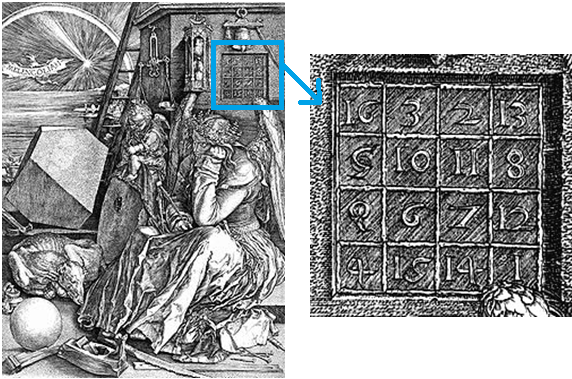
Co to jest kwadrat magiczny?Kwadrat magiczny to tablica liczb składająca się z n wierszy i n kolumn dla n >2 , w którą wpisano n2 różnych liczb naturalnych. Suma liczb w każdym wierszu, w każdej kolumnie i w każdej przekątnej jest taka sama i nazywa się sumą magiczną. Wyróżniamy również kwadraty półmagiczne czyli takie, w których suma liczb w każdym wierszu i każdej kolumnie jest taka sama, ale sumy liczb w przekątnych są różne. Kwadraty magiczne znali już starożytni Chińczycy i Hindusi, wierzyli w ich magiczną moc i dlatego umieszczali je na amuletach i talizmanach. Najsłynniejszym kwadratem magicznym jest jednak ten, który umieścił Albrecht Dürer na swoim słynnym miedziorycie "Melancholia I"(zobacz grafikę powyżej). Zapewne nieprzypadkowo w dwu wewnętrznych kratkach ostatniego wiersza tego kwadratu stoją obok siebie liczby 15 i 14, składające się na datę powstania grafiki – rok 1514. |
 |
ZagadkaSpróbuj ułożyć kwadrat magiczny 3 na 3. |
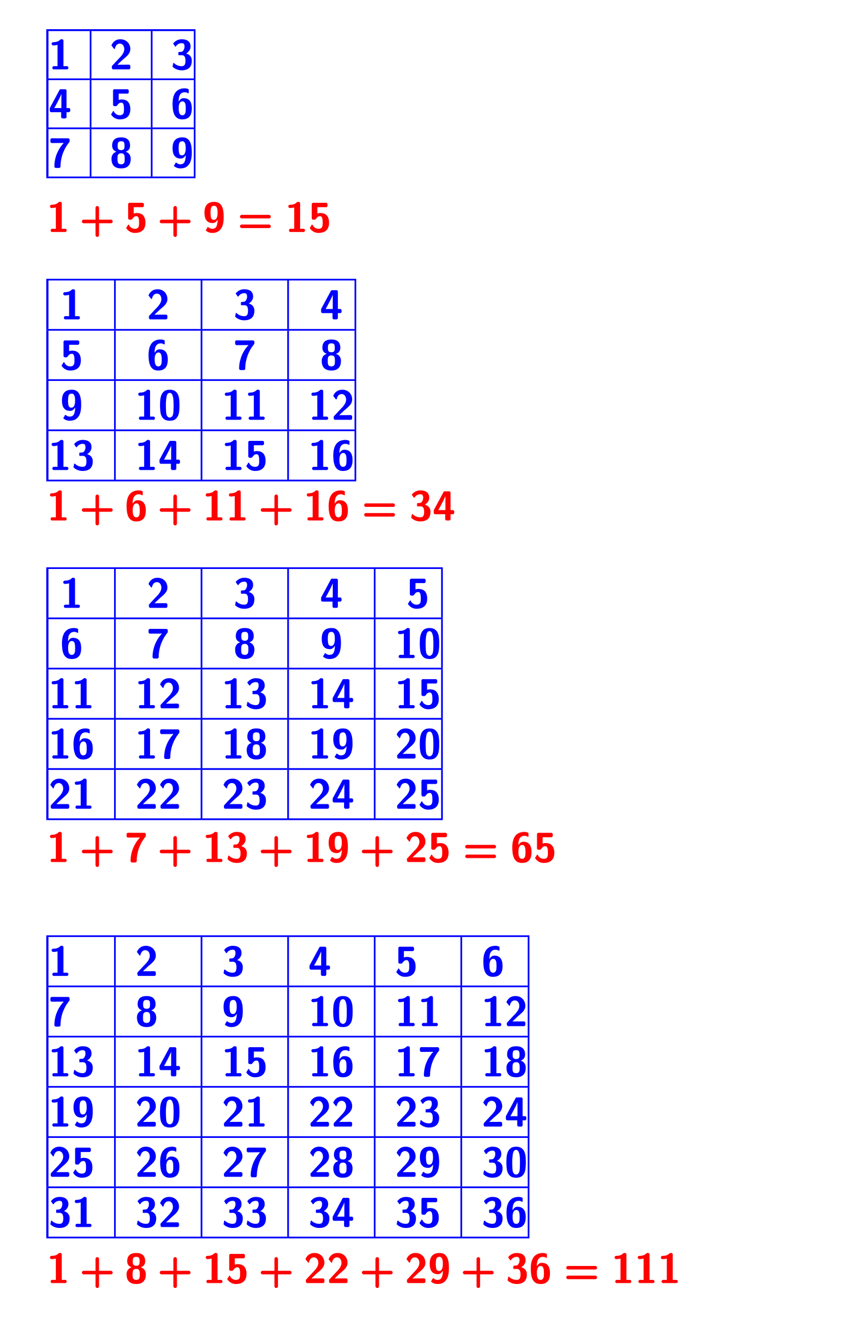
Sumy magiczne. Czy jest jakaś zależność?Mam nadzieję, że udało Ci się ułożyć kwadrat magiczny. Jednak dużo łatwiej układa się liczby w kwadracie, jeśli wiemy jaka powinna być suma w każdej kolumnie, wierszu i na obu przekątnych. W tym przypadku wynosiła ona 15. A jak będzie w kwadratach większych i czy istnieje jakaś zależność? Najłatwiej zaobserwować sumy magiczne dodając liczby po przekątnej zawierającej liczbę 1. Bardzo szybko zauważymy, że suma magiczna dla kwadratu 3 na 3 to 15, dla 4 na 4 - 34, 5 na 5 - 65, 6 na 6 - 111 itd. |
 |
Wzór na sumę magiczną
Sprawdźmy dla n=5
Jak widzimy wzór jest prawdziwy.
|
Zadanie
|
Widać, że ułożenie kwadratu 4 na 4 wiąże się z dużo większym wysiłkiem, chyba że posłużymy się jakimś algorytmem. Jak ułożyć kwadrat magiczny 4 na 4? |
Spróbuj jeszcze raz ułożyć kwadrat 4 na 4, a potem przejdź do gry, gdzie kwadrat ma rozmiar 5 na 5. |
Metoda hinduska układania kwadratów magicznych nieparzystychJak ułożyć kwadrat 5 na 5? A może jest algorytm? Oto jeden ze sposobów. Odtwórz planszę interaktywną i przeanalizuj, a potem jeszcze raz wybróbuj na kwadracie 3x3 i 5x5. |
Na konice spróbuj ułożyć kwadrat 6 na 6. Może też odkryjesz jakieś zależności. |