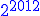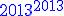Wstęp

Nasze przyzwyczajenia dotyczące liczenia są takie, że łatwo nam jeszcze wyobrazić sobie, że czegoś jest tysiąc czy kilka tysięcy, bo chociażby mamy takie doświadczenia w życiu codziennym przy używaniu pięniędzy. Z większych liczb możemy używać jeszcze czasem milionów i miliardów, ale to i tak raczej tylko w kontekście obserwacji wiadomości medialnych. Raczej nigdy sami nie policzyliśmy nawet do tysiąca, nie mówiąc już o milionie. A jednak wielkie liczby istnieją i się nimi musimy posługiwać, co więcej często potrzebujemy ich własności np. czy dana liczba jest parzysta, a może podzielna przez 3? Oczywiście epoka komputerów pomaga "obsługiwać" te wielkie liczby, ale może istnieją jakieś matematyczne skróty, żeby np. znajdować ostatnie cyfry wielkich potęg?

Eksperyment

Zróbmy mały eksperyment. Zapiszmy kilkanaście pierwszych potęg liczby 2, zaczynając od wykładnika 1. Proszę zwróć uwagę, że ostatnie cyfry kolejnych potęg liczby 2 to ciągle w tej samej kolejności te same cyfry:

2,4,8,6,...itd

Możemy więc mówić o tym, że ostatnie cyfry kolejnych potęg dwójki są cykliczne i zmieniają się co cztery!

Sprawdźmy, jaką ostatnią cyfrą jest cyfra liczby

W tym celu wystarczy sprawdzić resztę z dzielenia przez 4. W naszym przypadku liczba 2012 dzieli się przez 4, ponieważ liczba złożona z dwóch ostatnich cyfr jest podzielna przez 4, czyli ostatnią cyfrą liczby jest taka sama cyfra jak w czwartej potędze liczby 2, czyli jest nią cyfra 6.

Czy ostatnie cyfry kolejnych potęg wszystkich cyfr od 0 do 9 są cykliczne?

Cykliczność ostatnich cyfr kolejnych potęg liczby 2 jest już pewnością. A jak jest z innymi liczbami? Czy cykliczność też jest co cztery liczby czy może inaczej.

Posługując się planszą interaktywną zmieniaj suwakami podstawy potęg, a potem obserwuj, jak zmienia się ostatnia cyfra, gdy będziesz zmieniać wykładniki tych potęg. Czy też będzie występowała cykliczność?

Ostatnie cyfry potęg

Podsumowanie

Jak widać, możemy zrobić podsumowanie. Cykliczność występuje zawsze, ale jest różna. Może to być jedna cyfra jak przy potęgach o podstawie 0, 1, 5 czy 6, dwie cyfry, a może być ich najwięcej 4. Pokażmy to zestawienie w tabeli.

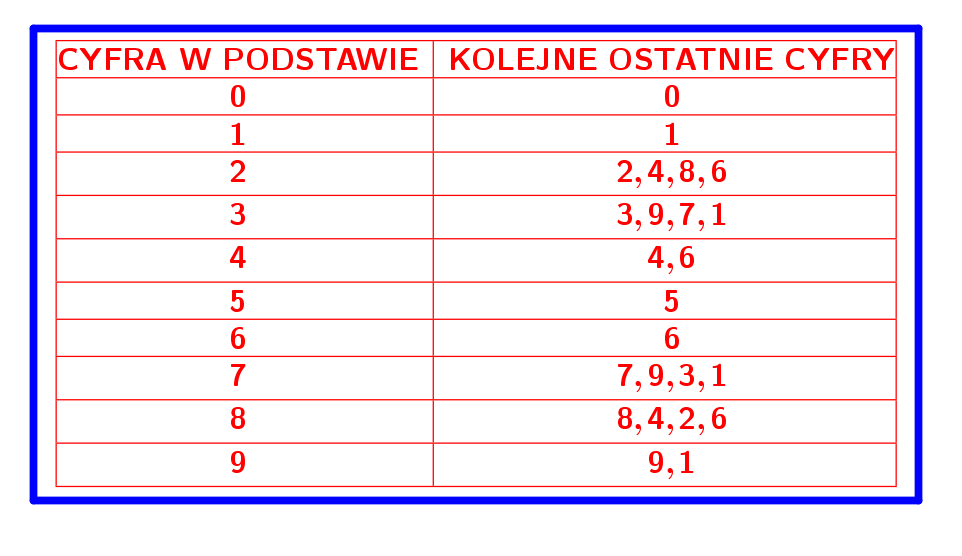Nie tylko duże wykładniki

Okazuje się, że cykliczność potęg, którą sprawdzaliśmy potęgując liczby jednocyfrowe z powodzeniem możemy przenieść na większe liczby. Sprawdźmy to na przykładzie potęgi:

Wystarczy spojrzeć, jaka jest ostatnia cyfra podstawy potęgi. W naszym przypadku jest nią cyfra 3, a więc cykliczność ostatnich cyfr to 3, 9, 7, 1. Liczba 2013 przy dzieleniu przez 4 daje resztę 1, co oznacza, że ostatnią cyfrą naszej potęgi jest cyfra 3. Przykład możemy sprawdzić, posługując się edytorem do wyznaczania ostatnich cyfr wielkich potęg.

Zadania do samodzielnego wykonania

Spróbuj wykorzystać poznane umiejętności w zadaniach. Powodzenia!