



Kwadratura koła i inne wielkie problemy matematyki
Autor
Dariusz Kulma |
Według Helleńskiej legendyDawno temu na greckiej wyspie Delos zapanowała straszliwa epidemia dżumy. Przerażeni mieszkańcy udali się do świątyni Apolla – opiekuna wyspy z pytaniem, co zrobić, by uratować ludność przed zagładą. Bóg zażądał, aby dwukrotnie powiększyć ofiarny ołtarz w kształcie sześcianu. Mieszkańcy szybko wykonali zadanie, stawiając na ten ołtarz jeszcze jeden taki sześcian. Mimo spełnienia rozkazu, dżuma dalej zbierała śmiertelne żniwo. Okazało się, że nie wolno było zmienić kształtu ołtarza. Apollo okazał się zbyt wymagający, a problem ten, czyli jak mając dany sześcian, skonstruować sześcian o dwukrotnie większej objętości, to pierwszy z problemów delijskich. Drugi to trysekcja kąta – czyli problem podzielenia kąta na trzy równe części za pomocą cyrkla i linijki. Trzeci, ostatni, to słynna kwadratura koła: jak, mając dane koło, skonstruować kwadrat o tym samym polu? Zagadnienia te to trzy główne nierozwiązalne zadania świata antycznego, a sama kwadratura koła przeszła do języka potocznego jako określenie właśnie takiego zadania. Omówmy w skrócie, na czym polegały niemożliwe do wykonania konstrukcje. |
Kwadratura koła Kwadratura koła to problem polegający na skonstruowaniu kwadratu, którego pole równe jest polu danego koła przy użyciu wyłącznie cyrkla i linijki bez podziałki. Rozważania rozpoczęli Pitagorejczycy, a wielu znanych i sławnych matematyków próbowało rozwiązać lub udowodnić brak rozwiązania. Dopiero w XIX wieku udało się przeprowadzić taki dowód. Najpierw w XVIII wieku Lambert wykazał niewymierność liczby
|
Trysekcja kątaTrysekcja kąta polega na podzieleniu dowolnego kąta na trzy równe części przy użyciu tylko cyrkla i linijki bez podziałki. Podobnie jak przy kwadraturze koła, niwykonalność tej konstrukcji udowodnił Pierre Wantzel w 1837 roku.
|
Podwojenie sześcianu Podwojenie sześcianu to zadanie polegające na zbudowaniu sześcianu o objętości dwa razy większej niż dany. Historia podwojenia sześcianu została przedstawiona w legendzie. Jest to konstrukcja niewykonalna, ponieważ nie można skonstruować boku o długości |


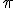 , co oznaczało, że liczby tej nie da się przedstawić za pomocą ułamka zwykłego. W 1837 roku Pierre Wantzel udowodnił niewykonalność, a dodatkowym potwierdzeniem był fakt swierdzony w 1882 roku przez Ferdinanda von Lindemanna, który w swoje trzydzieste urodziny podał, że
, co oznaczało, że liczby tej nie da się przedstawić za pomocą ułamka zwykłego. W 1837 roku Pierre Wantzel udowodnił niewykonalność, a dodatkowym potwierdzeniem był fakt swierdzony w 1882 roku przez Ferdinanda von Lindemanna, który w swoje trzydzieste urodziny podał, że ![\sqrt[3]{2} \sqrt[3]{2}](http://matematykainnegowymiaru.pl/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.gif) .
.