



Dwumian Newtona a trójkąt Pascala
Autor
Dariusz Kulma |
Dwumian NewtonaNieraz spotykamy się z wzorami typu
Przy każdym współczynniku mamy postać symbolu Newtona, który przyjmuje wzór:
Jednak stosowanie tego wzoru w praktyce, szczególnie przy rozbudowanych wyrażeniach nie jest wygodne. W dodatku nie każdy jeszcze w klasach młodszych spotkał się z symbolem silni n!. |
Trójkąt PascalaOkazuje się, że współczynniki symbolu Newtona tworzą specyficzny trójkąt. Zaobserwuj, zmieniając wykładniki kolejnych potęg wyrażenia |
Dwumian Newtona a trójkąt Pascala |
Co można zaobserować1°Kolejne wiersze powstają poprzez dopisywanie kolejnych 1 na bokach trójkąta, a poszczególne wyrazy wewnątrz trójkąta powstają przez dodawanie dwóch wyrazów z poprzedneigo wiersza znajdującęgo się nad wyrazem, który należy zapisać np. liczba 4 powstała z zsumowania liczby 1 i 3, które się nad tą liczbą znajdują. 2°Zawsze suma wykładników w kolejnych wyrażeniach jest równa n. 3°Kolejne wykładniki przy liczbie x maleją o 1 zaczynając od n, a kolejne wykładniki przy y rosną o 1 zaczynając od 0. 4°Jeśli pomiędzy x i y znajduje się "+", to wszystkie wyrażenia są dodatnie, a jeśli "-", to znaki piszemy przemiennie zaczynając od "+". |
ZadaniePosługując się zdobytą wiedzą rozpisz wyrażenie |
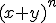 . Oczywiście jest wzór, który pozwala rozpisywać takie wyrażenia i nazywamy go Dwumianem Newtona. Oto on:
. Oczywiście jest wzór, który pozwala rozpisywać takie wyrażenia i nazywamy go Dwumianem Newtona. Oto on: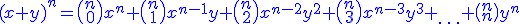
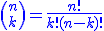
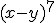 , a potem sprawdź za pomocą poniższej planszy czy dobrze zrobiłeś.
, a potem sprawdź za pomocą poniższej planszy czy dobrze zrobiłeś.