



Równanie zegara
Zegar z czasem rzeczywistym |
WstępLekcja będzie dotyczyła równania zegara, co brzmi zapewne dość zagadkowo. Pod tą tajemniczą nazwą kryje się obliczenie jaki kąt tworzą wskazówki (godzinowa i minutowa) o określonej godzinie. Można by było spróbować to zrobić przy pomocy kątomierza, ale obawiam się, że nie byłoby to wcale łatwe, a poza tym wyniki nie były dokładne. Wymyślono więc pewien wzór, za pomocą którego znając godzinę będziemy mogli obliczyć jaki dokładnie kąt jest pomiędzy wskazówkami. Spójrz na planszę poniżej i zobacz, w jaki sposób powstał ten bardzo pomocny wzór.
|
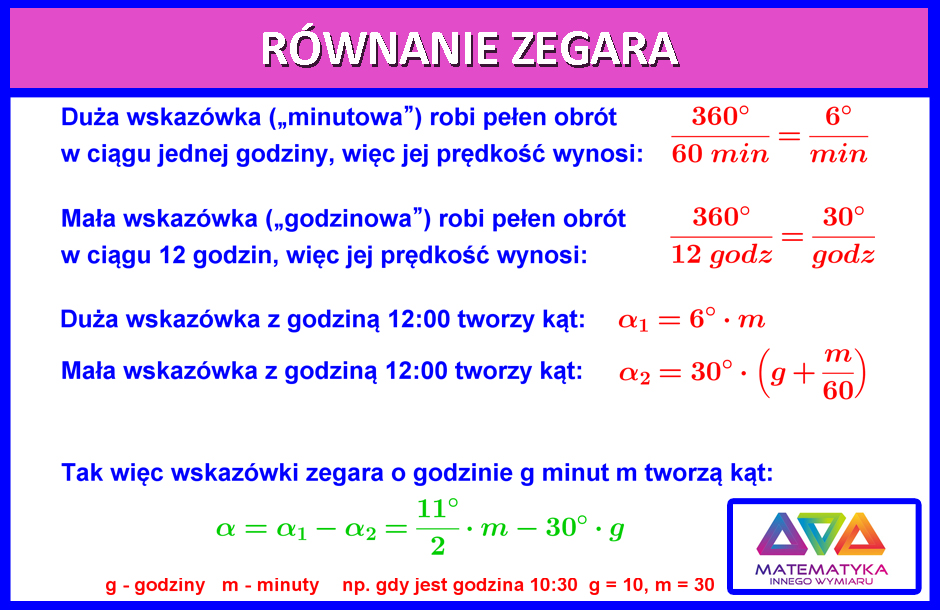
Równanie zegara
|
Ze wzoru wynikają następujące zależności: Kąt jest:
|
Rozwiązywanie zadańWykorzystajmy więc poznany wzór w praktyce i obliczmy, jaki kąt utworzą wskazówki o godzinie 11:45. Jeżeli nasza godzina to 11:45, oznacza to, że m = 45, g = 11 Podstawiając te wielkości do wzoru i po wykonaniu obliczeń otrzymujemy:
Z tego wynika, że kąt pomiędzy wskazówkami wynosi Żeby sprawdzić czy wykonaliśmy poprawne obliczenia skorzystamy z planszy, w której należy na zegarze ustawić poprawną godzinę i zaznaczyć pole wyboru "pokaż kąt między wskazówkami". |
Zegar |
Teraz samodzielnie rozwiąż jeszcze kilka przykładów obliczając jaki kąt między wskazówkami będzie o godzinie: 8:08, 10:20, 4:14 Możesz również wymyślać swoje własne przykłady, ustawiając godziny na zegarze. Pamiętaj jednak, by najpierw samodzielnie spróbować rozwiązać zadanie, a następnie sprawdzić swój wynik |
Kiedy wskazówki zegara będą w linii prostej ?Żeby wskazówki zegara były w linii prostej, kąt między nimi musi być równy 180o, co zapiszemy równaniem:
Przekształcamy równanie, by wyliczyć "m":
Ostatecznie:
Gdy mamy już taką postać równania, możemy za "g" podstawiać różne liczby oznaczające godziny i obliczymy w ten sposób, ile dokładnie powinno być wtedy minut, żeby wskazówki były w linii prostej. Np. Gdy Sprawdźmy inne wybrane przykłady: Gdy Gdy Gdy Jeśli przeprowadzilibyśmy nasze obliczenia dla wszystkich godzin, to okazałoby się, że wskazówki tworzą linię prostą bez ułamków w minutach tylko o godzinie 6:00. Możesz to sprawdzić korzystając z planszy z zegarem, jak w poprzednich zadaniach. |
A teraz zastanówmy się kiedy wskazówki zegara się pokryją ?Żeby wskazówki zegara się pokryły, kąt między nimi musi być równy 0o, co znów zapiszemy równaniem:
Przekształcamy równanie jak poprzednio, by wyliczyć "m":
Ostatecznie:
Gdy mamy już taką postać równania, rozpatrzmy różne przypadki dla dowolnych wartości "g". Np. Gdy Gdy Gdy Jeśli przeprowadzilibyśmy nasze obliczenia dla wszystkich godzin, to okazałoby się, że wskazówki tworzą linię prostą bez ułamków w minutach tylko o godzinie 0:00 oraz 12:00, które wiemy, że na zegarze są przedstawione przez taki sam układ wskazówek. W tym przypadku również możesz to sprawdzić korzystając z planszy z zegarem, jak w poprzednich zadaniach. |
Na koniec rozwiążmy jeszcze kilka zadań z portalu. Już teraz nie powinieneś/powinnaś mieć żadnych problemów. Powodzenia! |
 | Zadanie 98 - W matwieży jedne drzwi mają niesamowitą ... |
 | Zadanie 362 - Król Pierwiastkus Wielki chciał zaprosić ... |
 | Zadanie 905 - Główne wiadomości informacyjne telewizji ... |
 | Zadanie 66 - Na ratuszowej wieży Deltoigrodu zawsze, ... |



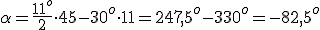
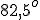 i mała wskazówka (czyli godzinowa) wyprzedza dużą wskazówkę (minutową).
i mała wskazówka (czyli godzinowa) wyprzedza dużą wskazówkę (minutową).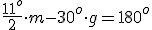
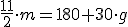
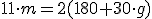
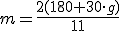
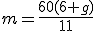
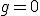 , to
, to 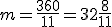 , więc otrzymujemy godzinę
, więc otrzymujemy godzinę 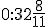 , co oznacza, że wskazówki będą w linii prostej, gdy miną
, co oznacza, że wskazówki będą w linii prostej, gdy miną 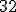 pełne minuty i jeszcze
pełne minuty i jeszcze 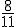 kolejnej minuty po północy lub po 12:00.
kolejnej minuty po północy lub po 12:00.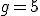 , to
, to 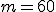 , więc otrzymujemy godzinę
, więc otrzymujemy godzinę 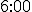 , co oznacza, że wskazówki będą w linii prostej dokładnie o tej godzinie.
, co oznacza, że wskazówki będą w linii prostej dokładnie o tej godzinie.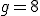 , to
, to 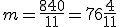 , więc otrzymujemy godzinę
, więc otrzymujemy godzinę 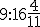 , ponieważ
, ponieważ 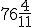 dają nam jedną pełną godzinę oraz
dają nam jedną pełną godzinę oraz 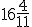 minuty.
minuty.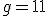 , to
, to 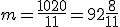 , więc otrzymujemy godzinę
, więc otrzymujemy godzinę 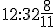 , ponieważ
, ponieważ 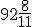 dają nam jedną pełną godzinę oraz
dają nam jedną pełną godzinę oraz 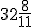 minuty.
minuty.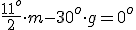
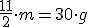
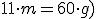
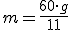
 , więc otrzymujemy godzinę
, więc otrzymujemy godzinę 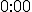 , co oznacza, że wskazówki pokryją się dokładnie o tej godzinie.
, co oznacza, że wskazówki pokryją się dokładnie o tej godzinie.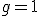 , to
, to 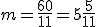 , więc otrzymujemy godzinę
, więc otrzymujemy godzinę 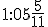 , co oznacza, że wskazówki pokryją się, gdy minie pięć pełnych minut jeszcze
, co oznacza, że wskazówki pokryją się, gdy minie pięć pełnych minut jeszcze 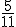 minuty po godzinie
minuty po godzinie  .
. .
.