



Niestandardowe cechy podzielności
Autor
Dariusz Kulma |
Podstawowe cechy podzielnościWiększość pamięta na pewno podstawowe cechy podzielności. Dobrze wiemy, kiedy liczba dzieli się przez 2 czy 5. Przypomnijmy jednak kilka podstawowych cech podzielności.
|
Cechy podzielności przez liczby od 2 do 10
|
Łączenie cech podzielności dzielników względnie pierwszychCechy podzielności można łączyć i wykorzystywać do sprawdzania podzielności przez liczby większe. Dobrze wiemy, że jeśli liczba dzieli się przez 2 i 3, to dzieli się również przez iloczyn tych liczb czyli 6. Takich cech można podać bardzo wiele. Warunek jest jednak taki, aby dzielniki były względnie pierwsze względem siebie. Przykładowo liczba 40 dzieli się przez 2 i przez 8, ale to wcale nie oznacza, że 40 dzieli się przez iloczyn 2 i 8 czyli 16. Dzieje się tak dlatego, że 2 i 8 nie są liczbami względnie pierwszymi. Przypomnijmy definicję liczb względnie pierwszych. |
Liczby względnie pierwsze
|
Wyprowadzanie cech podzielnościJeśli wiemy już, że możemy stwierdzić, że liczba dzieli się przez iloczyn liczb względnie pierwszych, to możemy tworzyć wiele cech podzielności. Przykładowo liczba dzieli się przez:
Tylko pozostaje problem - kiedy liczba dzieli się przez 7 albo 11? Okazuje się, że jest wiele cech mniej standardowych niż używane na codzień. Podzielność przez 7, 11, 13 czy 37 są bardzo użyteczne w zadanaich o podwyższonym stopniu trudności. Oto kilka ważnych cech na planszach inetraktywnych i statycznych. |
Cecha podzielności przez 7 |
Cecha podzielności przez 11 |
Cecha podzielności przez 13
|
Cecha podzielności przez 37
|
Cecha podzielności przez 101
|
Cecha podzielności przez 143
|
Cecha podzielności przez 1001
|
Zadanie interaktywneWłącz poniższe zadanie interaktywne i sprawdź czy już potrafisz korzystać z cech podzielności przez 7, 11, 13 czy 143. Pamiętaj, że czasami szybciej sprawdzisz cechę podzielności przez 143 niż oddzielnie przez czynniki tego dzielnika 11 i 13. Powodzenia! |
Zadania z portalu MIWA teraz garść zadań konkursowych. Postaraj się wykorzystać zdobytą wiedzę jak najlepiej. |
 | Zadanie 166 - Najgroźniejszy matprzestępca Kwadratolandii ... |
 | Zadanie 170 - W Kwadratolandii każde słowo mieszkańcy ... |
 | Zadanie 172 - Reszta z dzielenia liczby 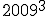 ... ... |
 | Zadanie 175 - Zakrzewek zastanawiał się ostatnio, ile ... |
 | Zadanie 573 - Liczba 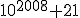 podzielna ... podzielna ... |
 | Zadanie 594 - Podane liczby podzielne przez 7, niezależnie ... |
 | Zadanie 653 - Dana jest liczba sześciocyfrowa CBACBA. ... |
 | Zadanie 130 - W Kwadratolandii każde słowo mieszkańcy ... |
 | Zadanie 452 - Różniczka zakochała się w Czesiu Iloczyńskim. ... |
 | Zadanie 531 - Wartość wyrażenia 2008 - 2007 + 2006 ... |
 | Zadanie 769 - Wymierniak oznaczył przez A zbiór czynników ... |
 | Zadanie 825 - Matcyfrzak zna cechy podzielności przez ... |
 | Zadanie 937 - Najbardziej szczęśliwa liczba w Kwadratolandii ... |
 | Zadanie 422 - Wyrażenie 12n+6, gdzie n jest liczbą ... |








