



Po co nam całki?
Autor
Dariusz Kulma |
Całka, co to takiego?Nie jest łatwo w kilku słowach zdefiniować całkę. Najprościej można powiedzieć, że jest to pojęcie odwrotne do liczenia pochodnych, Mówimy czasami o całce, że jest to funkcja pierwotna czyli, że jeśli najpierw z jakiejś funkcji policzymy pochodną, a potem obliczymy całkę, to powinniśmy uzyskać dokładnie to samo wyrażenie. Sprawdźmy. Weźmy wyrażenie Korzystając z wzoru
Całki mają bardzo szerokie zastosowanie w wielu dziedzinach: fizyce, chemii i wielu innych. Jedno z podstawowych zastosowań całki to liczenie pól powierzchni, długości łuków czy objętości kształtów nieregularnych czyli takich, które ciężko jest wyliczyć z podstawowych wzorów. Popatrzmy na planszę z całką oznaczoną czyli taką, która jest określona między jakimiś dwoma argumentami. Całka oznaczona jest równa wartości między funkcją a osią OX w tym przedziale. |
Całka oznaczona
|
Jak widać, aby policzyć powierzchnię między między funkcją a osią OX, należy policzyć całkę funkcji (F(x)), a następnie obliczyć różnicę tej funkcji pierwotnej dla argumentów, które ograniczają to pole. |
Całka nieoznaczonaBy mówić jednak o całce oznaczonej i obliczać pola powierzchni, musimy nauczyć się obliczać całki nieoznaczone. Wzorów jest bardzo dużo. Na poniższych planszach znajdziesz wszystkie najważniejsze. W planszy interaktwnej zmieniaj podstawę i wykładnik potęgi, by zobaczyć jak się zmienia wartość całki. |
Całka nieoznaczona |
Całki funkcji elementarnych, cz.1
|
Całki funkcji elementarnyh, cz.2
|
Całkowanie przez podstawienieJest to sposób całkowania, w którym podstawiamy zmienną za jakiś fragment naszego wyrażenia znajdującego się pod całką. Obliczamy ją posługując się zmienną i wracamy znowu do wcześniejszego wyrażenia. Poniżej kilka przykładów dotyczących podstawienia, które możesz oglądać krok po kroku. |
Całkowanie przez częściMetoda, w której trudno jest obliczyć zadaną całkę, a po zastosowaniu wzoru:
|
Obliczanie pola pod funkcjąNa początek spróbujmy obliczyć pole pod funkcją liniową w określonych granicach. Obejrzyj poniższą planszę.
|
A teraz trochę trudniejszy przykład - policzymy pole pod funkcją sinus w przedziale od zera do pi. Obejrzyj planszę krok po kroku. |
A teraz pole trochę między dwoma funkcjami. Należy od pola pod jedną funkcją odjąć pole pod drugą funkcją. W praktyce od funkcji z wyższymi wartościami odejmujemy funkcję z niższymi. Obejrzyj przykład w zadaniu interaktywnym. |
Jak już wspominaliśmy, całki można wykorzystywać do obliczenia wielu wartości np. pola powierzchni bocznej brył obrotowych. Obejrzyj planszę statyczną.
|
ZadaniaNa koniec kilka zadań z portalu MIW. |
 | Zadanie 995 - Pole zawarte między wykresem funkcji ... |
 | Zadanie 1173 - Pochodna wyrażenia 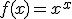 ... ... |
 | Zadanie 1186 - Całka 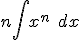 ... ... |
 | Zadanie 1187 - Pole obszaru między parabolą 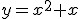 ... ... |
 | Zadanie 1188 - Pole między prostą 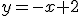 ... ... |
 | Zadanie 1189 - Wartość całki 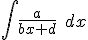 ... ... |
 | Zadanie 1190 - Wartość całki 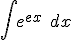 ... ... |
 | Zadanie 1191 - Pole między osią Ox a funkcją sin x w ... |
 | Zadanie 1192 - Pochodna całki ... |
 | Zadanie 1193 - Wartość całki [tex]\int_{2p}^{2t}{ }\;cos\;x\;dx[/... |
 | Zadanie 1194 - Funkcję homograficzną 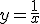 ... ... |
 | Zadanie 1197 - Wartość 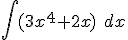 ... ... |
 | Zadanie 1198 - Pole obszaru ograniczonego funkcjami ... |


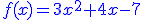 . Pochodna tej funkcji wyniesie:
. Pochodna tej funkcji wyniesie: 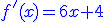 . Teraz spróbujmy wrócić.
. Teraz spróbujmy wrócić.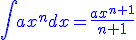
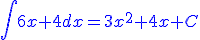 Jak widać nie wiadomo co wstawić jako stałą. Wcześniej było -7, a teraz musieliśmy napisać w sposób symboliczny C. Funkcja jest jednak taką samą funkcją dla C=-7.
Jak widać nie wiadomo co wstawić jako stałą. Wcześniej było -7, a teraz musieliśmy napisać w sposób symboliczny C. Funkcja jest jednak taką samą funkcją dla C=-7.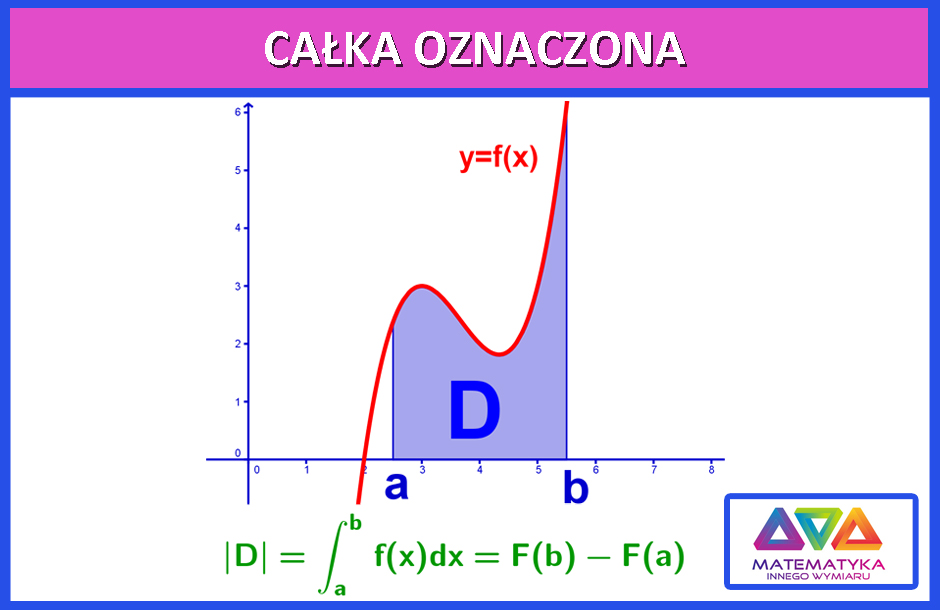



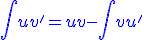 , gdzie u' i v' oznaczają pochodne funkcji u i v, obliczenie staje się dużo łatwiejsze. Obejrzyj kilka przykładów na poniższej planszy.
, gdzie u' i v' oznaczają pochodne funkcji u i v, obliczenie staje się dużo łatwiejsze. Obejrzyj kilka przykładów na poniższej planszy.