



Układanki z patyczków
Autor
Agnieszka Rogalska |
|
Pierwsza nasza zagadka dotyczy sześcianu. Zadanie polega na tym, żeby za pomocą trzech dodatkowych patyczków stworzyć widok rzutu sześcianu. Zastanów się jak możemy to zrobić? |
Jeśli masz problem z tym zadaniem, to pomocny będzie aplet z widokiem sześcianu. W pierwszym z podanych poniżej widoczne są tylko krawędzie, a w drugim również ściany boczne. Możesz skorzystać z dowolnego. Spróbuj za pomocą uchwytu tak ustawić nasz sześcian, żeby jego krawędzie zewnętrzne utworzyły figurę jak na początku zagadki (czyli sześciokąt), a zobaczysz, że krawędzie w środku figury same pokażą Ci rozwiązanie zagadki. Należy tylko pamiętać, że interesują nas wyłącznie krawędzie widoczne, czyli te narysowane linią ciągłą. |
Ułóż teraz w ten sam sposób patyczki w zagadce i sprawdź swoje rozwiązanie. |
W kolejnej łamigłówce również mamy podobną figurę jak w poprzedniej, ale tym razem naszym zadaniem jest przestawić dwa patyczki i dodać jeden, żeby ułożyć dwa romby. Powodzenia! |
Jeśli nie udało Ci się rozwiązać łamigłówki, to pomyśl, ile boków ma romb? Zgadza się - cztery. Żeby zbudować dwa romby, potrzebujemy więc ośmiu patyczków. Jak to zrobić, skoro mamy ich tylko siedem? Połamać? Nie, wystarczy dwa romby zbudować w ten sposób, by miały jeden wspólny bok. Teraz powinno być łatwiej, sprawdź swoje rozwiązanie. Jeżeli obróciłeś/łaś dwa sąsiednie patyczki do środka i dołożyłeś/łaś jeden, a Twój rysunek wygląda inaczej niż w odpowiedzi, to nie martw się, ponieważ wszystkie takie rozwiązania są poprawne. No właśnie, ile jest możliwości ułożenia dwóch rombów w ten sposób? |
Trzecia łamigłówka dotyczy symetrii. Musimy przestawić trzy patyczki i oko ryby w ten sposób, żeby płynęła w przeciwnym kierunku. Do dzieła! |
Udało się? Jeśli nie, to przeczytaj podpowiedź. Jeśli ryba ma płynąć w przeciwnym kierunku, to jej obraz powinien być odbiciem poprzedniej ryby względem pionowej osi. Jeśli tak chcemy zrobić, wówczas musielibyśmy przesunąć cztery zapałki. |
Czwarta układanka jest nieco trudniejsza, ale spróbuj na początek jak zwykle rozwiązać ją bez podpowiedzi. Powodzenia! |
Przypomnij sobie drugą łamigłówkę. Tam również mieliśmy mniej patyczków, niż było potrzeba do ułożenia wszystkich boków figur oddzielnie. W tym zadaniu musimy myśleć podobnie, ponieważ mamy osiem patyczków, a chcąc zbudować oddzielnie cztery trójkąty i dwa kwadraty, potrzebowalibyśmy ich aż 20. Wynika z tego, że niektóre patyczki będą musiały należeć do kilku figur. Poszukaj takiego rozwiązania, w którym trójkąty będą miały boki zawarte zarówno w jednym jak i w drugim kwadracie. |
W piątej łamigłówce mamy dwa kwadraty zbudowane łącznie z 16 patyczków. Naszym zadaniem jest przestawić cztery z nich, żeby otrzymać trzy kwadraty. To zadanie ma kilka rozwiązań, warto więc poszukać różnych możliwości. Pamiętaj, że kwadraty mogą mieć wspólne całe boki lub ich część. |
W kolejnym zadaniu musimy z osiemnastu patyczków ułożyć dwa prostokąty o tej samej długości podstawy w taki spobób, by jeden z nich miał pole dwukrotnie większe od pola drugiego. |
Zadanie szóste można rozwiązać układając patyczki, ale możemy również podejść do niego algebraicznie. |
Jak już algebraicznie rozwiązaliśmy zadanie szóste, to spróbuj teraz rozwiązać następujące zadanie: Czy jest możliwe z tej samej ilości patyczków (18) zbudować takie dwa prostokąty, aby długość podstawy i pole jednego z nich były dwukrotnie większe niż długość podstawy i pole drugiego czworokąta.Do rozwiązania zadania możesz również wykorzystać patyczki z zadania szóstego.
A oto rozwiązanie algebraiczne powyższego zadania: Na początek należy zauważyć pewną zależność. W tym celu możesz otworzyć planszę z przypomnieniem wzoru na pole prostokąta. |
Korzystając z naszej planszy możemy zauważyć, że jeśli pole pierwszego prostokąta to P = a x b, a pole drugiego prostokąta miałoby być równe 2P = 2a x c, to b = c. To oznacza, że w naszym przypadku wysokości obu prostokątów muszą być takie same. Zatem: Pozostaje więc „18 - 6x” patyczków, które musimy podzielić na cztery pozostałe boki w obu prostokątach. |
Kolejna układanka to również kolejne wyzwanie algebraiczne. Zanim zaczniesz układać patyczki, spróbuj ułatwić sobie zadanie rachunkowo. Oto treść zadania: Z 18 patyczków zbuduj dwa prostokąty, których pola są takie same, a podstawy jednego prostokąta są:a/ dwa razy dłuższeb/ trzy razy dłuższec/ cztery razy dłuższeod podstawy drugiego prostokąta.A jak zadanie rozwiązać, zastępując prostokąty równoległobokami? Oznaczmy na odpowiednich bokach prostokątów ilość użytych patyczków, tak jak na rysunku poniżej. |
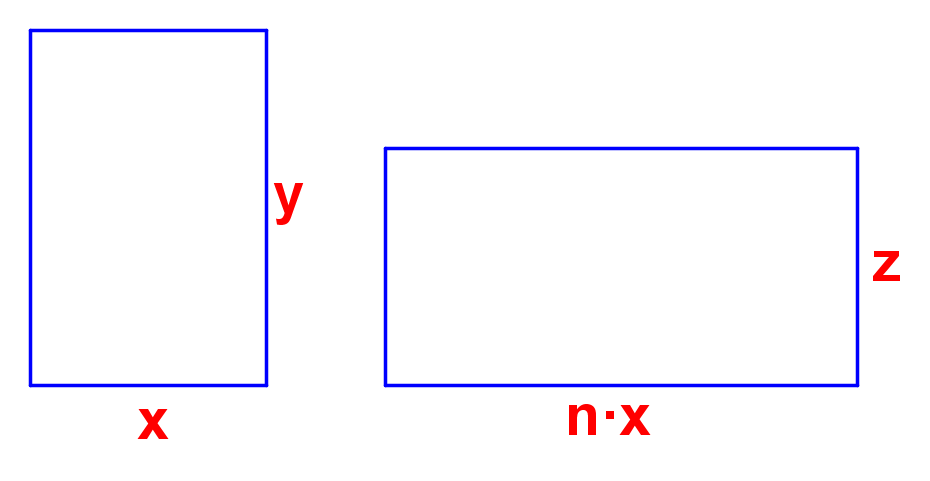 |
a/ Niech n=2. Suma obwodów obu prostokątów wynosi wówczas: 2x+4x+2y+2z = 18. Ponieważ xy = 2xz (bo pola są równe), więc: y = 2z Równanie 1 przyjmie postać 6x + 6z = 18, czyli z = 3-x Dla x = 1, z = 2, y = 4 mamy prostokąty: 1x4 oraz 2x2 Dla x = 2, z = 1, y = 2 mamy prostokąty: 2x2 oraz 4x1 (to poprzedni przypadek) Dla x = 3, z = 0, y = 0 co oznacza, że nie ma prostokąta. b/ Niech n=3 Suma obwodów obu prostokątów wynosi: 2x+6x+2y+2z=18 Ponieważ xy = 3xz, więc y = 3z Zatem 8x+8z = 18, czyli z=⅛ (18-x), a to nie jest liczba naturalna. Zatem nie ma prostokąta o polu trzykrotnie większym od pola drugiego prostokąta. c/ Dla n=4 też nie ma rozwiązania. |
Na koniec zostały nam jeszcze trzy ostatnie łamigłówki. Rozwiąż je samodzielnie. Czasem kilka rozwiązań może być prawidłowych, więc spróbuj znaleźć jak najwięcej z nich. Powodzenia! |




