



A gdyby tak konstruować długości niewymierne
Autor
Dariusz Kulma |
WstępW matematyce nie mamy problemu z rysowaniem długości, które są liczbami naturalnymi. Łatwo nam narysować odcinek o długości 3 cm czy 4 dm. Trochę lepszych narzędzi potrzeba, by odcinki miały długości wymierne. To tylko kwestia odpowiednich i w miarę dokładnych narzędzi. Jednak nieraz na pewno rysowaliśmy odcinek o długościach, które były chociażby ułamkami dziesiętnymi jak 5,2 cm czy 9,9 cm. Problemy pojawiąją się jednak, gdy trzeba narysować odcinek o długości niewymiernej np: |
Przekątna kwadratu jakaś niewspółmiernaPitagorejczycy mieli ogromny problem mierząc przekątną kwadratu. Liczbę, która im wychodziła, ale do niczego nie pasowała, nazwali niewspółmierną, ponieważ nie byli w stanie przedstawić tej liczby jako ilorazu dwóch liczb całkowitych. To właśnie Jednak najważniejsze, że rysowanie |
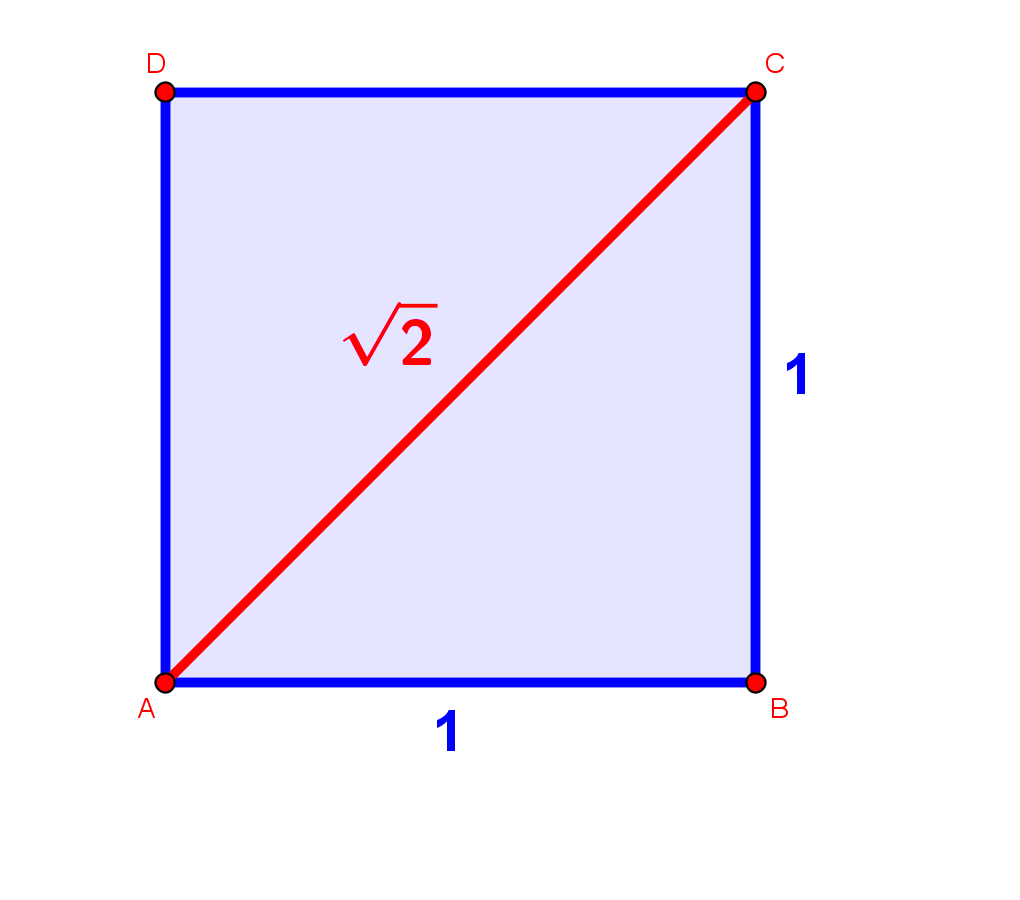 |
Teodoros z CyrenyPrzez długi czas jedyną liczbą niewymierną był pierwiastek z 2. Platon w swoim dziele Theaetetus opisuje, że jego nauczyciel matematyki, Teodoros z Cyreny, jako pierwszy wykazał niewymierność innych pierwiastków. Rozważał on pierwiastki:
Dzięki twierdzeniu Pitagorasa można przeprowadzić konstrukcję takich odcinków, których długości będą kolejnymi pierwiastkami kwadratowymi. Można je przedstawić za pomocą trójkątów prostokątnych, które tworzą swoistą spiralę, nazywaną potocznie spiralą Teodorosa. Zobacz założenia konstrukcji w poniższej planszy interaktywnej. |
Ślimak Teodorosa - konstrukcja odcinków o długościach będących pierwiastkami liczb naturalnych |
Wykonanie konstrukcji odcinka o długości niewymiernejWykonaj konstrukcyjnie, patrząc na poniższą planszę, konstrukcję odcinka o długości |
Pominąć spiralę TeodorosaMam nadzieję, że udało Ci się wykonać konstrukcyjnie odcinek o długości |



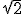 czy
czy 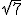 . I czy w ogóle jest to możliwe w prosty sposób? Przecież
. I czy w ogóle jest to możliwe w prosty sposób? Przecież 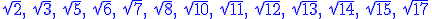

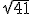 czy
czy 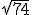 . Przy spirali Teodorosa rysowanej od samego początku byłoby to niemożliwe.
. Przy spirali Teodorosa rysowanej od samego początku byłoby to niemożliwe.