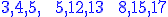Twierdzenie Pitagorasa
Autor
Dariusz Kulma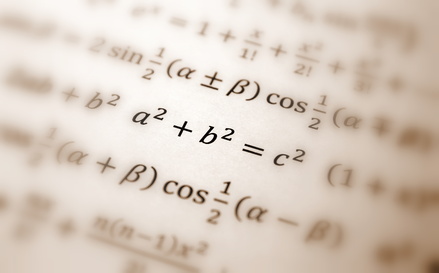 |
WstępMyli się ten kto myśli, że najbardziej znane twierdzenie na świecie dotyczące geometrii czyli twierdzenie Pitagorasa zawdzięczamy tylko samemu Pitagorasowi. Dokumenty pozostałe po niezależnie rozwijających się cywilizacjach Babilonu czy Egiptu pokazują, że zależności boków w trójkątach prostokątnych były znane już dużo wcześniej. Pitagoras - super gwiazda matematyczna starożytnych czasów zaczął jednak tę wiedzę porządkować i za Talesem udowadniać zaobserwowane twierdzenia. Zauważmy, że Pitagoras długo podróżował, odwiedzając zarówno Babilonię jak i Egipt. Oczywiście nie można odebrać mu chwały za uprządkowanie tych obserwacji i sformułowanie tego twierdzenia, jednak pokazuje to, że rozwój cywilizacyjny wymusza niejako odkrycia matematyczne. Oto kilka słów o tym wielkim matematyku. |
Pitagoras
|
Obejrzyj planszę interaktywną i przyjrzyj się na czym polega twierdzenie Pitagorasa. Zmieniaj długości przyprostokątnych i obserwuj obliczenia, potwierdzające zależność zawartą w twierdzeniu Pitagorasa. |
Twierdzenie Pitagorasa |
Babiloński Plimpton 322Może Cię zaskakiwać jakaś dziwna nazwa z numerem, ale wśród odnalezionych 500 tysięcy glinianych tabliczek pochodzących z Babilonu sprzed niemal 3500 lat 300 dotyczy matematyki. Jedną z najsławniejszych jest tabliczka Plimpton 322 (patrz zdjęcie poniżej). Nazwa pochodzi od nazwiska amerykańskiego dziennikarza George'a Arthura Plimptona, który oznaczył ją numerem 322 w swojej kolekcji. Tabliczka wypełniona znakami pisma klinowego zawiera cztery kolumny, które wydają się liczbami zapisanymi w sześćdziesiątkowym układzie pozycyjnym. Okazuje się, że wśród tych liczb znajdują się trójki pitagorejskie czyli liczby spełniające twierdzenie Pitagorasa. Oto kilka z nich:
Nie byłoby w tym nic dziwnego, gdyby nie fakt, że tabliczka datowana jest na przedział czasowy ok. 1800-1600 r. p.n.e. - ponad 1000 lat przed narodzinami Pitagorasa!!! |
 |
Egipski papirus RhindaDrugą wspaniale rozwijającą się cywilizacją był Egipt. Po Egipcjanach również zachowało się dużo dokumentów, ale w odróżnieniu od Babilończyków używali oni do zapisu papirusu. O dziwo sprzyjający klimat pozwolił by zachowały się one w bardzo dobrym stanie. Najlepszym odzwierciedleniem tego, co działo się w egipskim matematycznym świecie, jest papirus Rhinda (patrz zdjęcie poniżej). Nazwa pochodzi od odkrywcy papirusa, szkockiego egiptologa Henry'ego Rhinda w 1858 roku. Jest to zbiór 87 zadań arytmetycznych i geometrycznych, jakimi zajmowali się Egipcjanie, a powstał ok. 1650 roku p.n.e. Papirus Rhinda zawiera rozwiązanie krok po kroku, nawet ze szkicami rysunków. Spisał go skryba Ahmes, ale podał on również informację, że nie jest autorem, lecz tylko kopiował starszy dokument z około 1800 roku p.n.e. Wydawać by się mogło, że budowniczy niewyobrażalnie wielkiej jak na tamte czasy Piramidy Cheopsa musieli znać również zasady, jakimi rządzą się trójkąty prostokątne. A jak w papirusie Rhinda nic o tym nie ma, mimo że przypuszcza się, że zawarte w nich zadania musieli sobie przyswoić skrybowie królewscy. |
 |
Czy oznacza to, że jednak Egipcjanie nie wiedzieli nic o własnościach trójkąta prostokątnego? Nic bardziej mylnego. Po każdym wylewie Nilu Egipcjanie na nowo mierzyli swoje działki rolne. Na zalanych terenach rozmywały się miedze i trzeba było wyznaczać pola na nowo, a od powierzchni pola zależały też podatki. Jedną z podstawowych miar powierzchni był prostokąt o wymiarach łokieć na 100 łokci. Jednak do dokładnego wyznaczenia tego prostokąta potrzebny był kąt prosty. Okazało się, że Egipcjanie mają do tego znakomite narzędzie. Wiązali w równych odstępach węzły i tworzyli z nich trójkąt o bokach składających się z 3, 4, 5 węzłów, zauważając tym samym, że największy kąt jest kątem prostym! (patrz ilustracja poniżej) |
 |
Odtąd trójkąt o bokach 3, 4, 5 nazywamy trójkątem egipskim i jest on chyba jednym z najczęstszych przykładów używanych na lekcjach i w podręcznikach. |
Trójkąt egipski
|
Pitagorejczycy zauważyli, że trójkątów, w których boki są długościami naturalnymi, jest wiele. Trójkąty takie w obecnych czasach nazywamy pitagorejskimi i jest ich nieskończenie wiele. Otwórz planszę interaktywną i zobacz, za pomocą jakich wzorów można tworzyć trójki pitagorejskie. |
Jak widać sami możemy tworzyć za pomocą wzorów trójki pitagorejskie. Oto te najbardziej popularne i przydatne. |
Trójki pitagorejskie
|
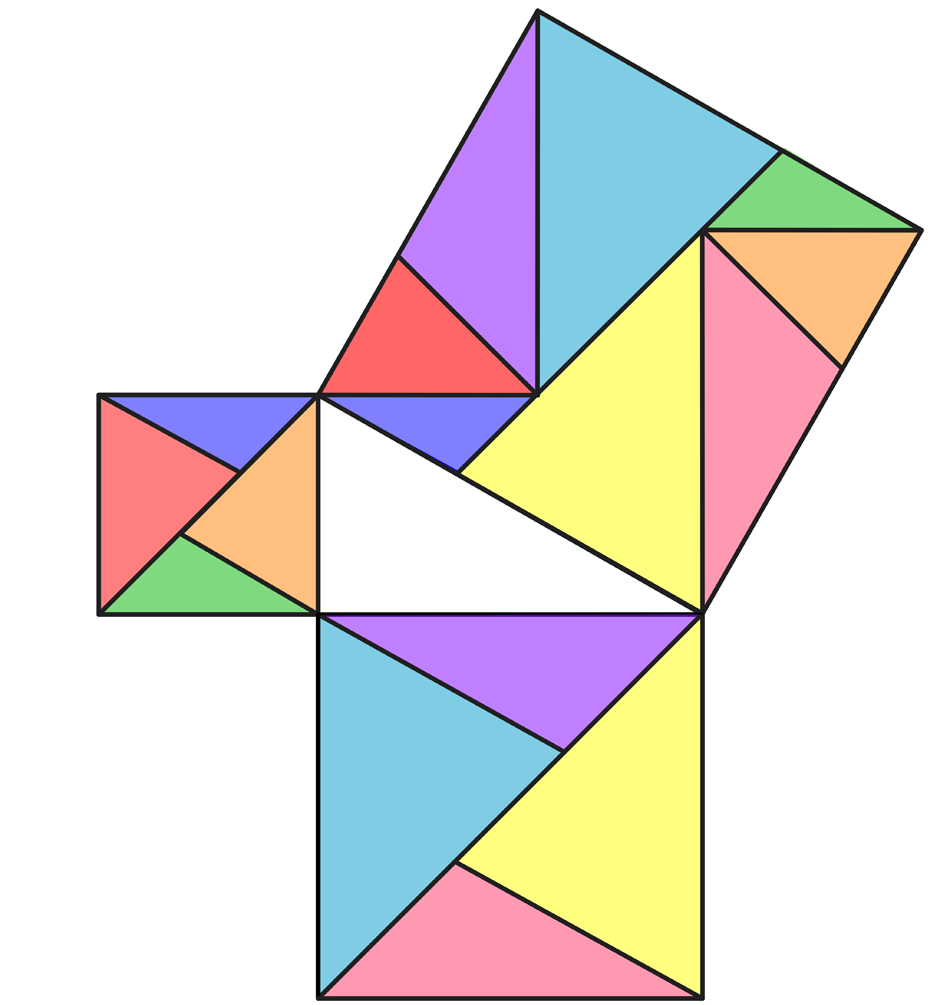
Dowody na twierdzenie PitagorsaWielu matematyków prześcigało się w udowadnianiu na nowe sposoby twierdzenia Pitagorasa. Podstawowy dowód przedstawiliśmy już w pierwszej planszy, budując kwadraty na bokach trójkąta prostokątnego i licząc ich pola. Obejrzyj animację z jednym z dowodów za pomocą rozcinania na części mniejszych kwadratów i układania z nich kwadratu zbudowanego na przeciwprostokątnej. |
I jeszcze inny przykład. |
 |