



O ciągach
Autor
Dariusz Kulma |
Ciągi liczbowe to listy liczb, które ułożono w określonej kolejności — według jakiejś zasady.Pierwszym ciągiem liczbowym, jaki człowiek zapisał, jest ciąg liczb naturalnych: 1, 2, 3, 4, 5, …. Każda kolejna liczba jest większa od poprzedniej o 1. Podobnie możemy ułożyć zbiór liczb parzystych czy podzielnych przez 3. To prostsze przykłady ciągów. Oczywiście istnieją ciągi bardziej skomplikowane. Dzięki zasadzie, która „rządzi” danym ciągiem, możemy obliczać dużo szybciej zależności między dowolnymi liczbami ciągu.Wyobraź sobie taki przykład (możesz też spróbować wykonać to doświadczenie). Weź arkusz papieru, jak największy, np. z gazety, i zacznij składać go na pół, potem jeszcze raz na pół itd. Jaką grubość będą mieć łącznie złożone warstwy, gdy złożysz ten arkusz 20 razy, a jaką gdy złożysz go 42 razy? Arkusz ma grubość ok. 0,1 mm. Po pierwszym złożeniu grubość wynosi 0,2 mm, po drugim — 0,4 mm, po trzecim — 0,8 mm, po czwartym — 1,6 mm. Nic szczególnego, prawda? Przy każdym złożeniu grubość zwiększa się dwukrotnie. Próbujemy jednak dalej. Składamy piąty raz — 3,2 mm, szósty — 6,4 mm, siódmy — 12,8 mm. W praktyce trudno złożyć ten arkusz więcej niż 6 – 7 razy, co już pewnie zauważyłeś. Jednak zasada, która rządzi narastaniem grubości tego złożonego arkusza, pozwoli nam obliczyć jego grubość po 20 czy 42 złożeniach. Zauważ, że pomijając przecinki w otrzymanych wynikach, otrzymujemy kolejne potęgi liczby Jednym z najbardziej tajemniczych i przedziwnych ciągów jest ciąg Fibonacciego.Leonardo Pisano Fibonacci żył w latach ok. 1175 — 1250 n.e. W 1202 roku wydał książkę Liber abaci (Księga abaku). Uczony poruszył w niej takie tematy, jak: podzielność, teoria liczb, symbolika matematyczna, ale również zasady księgowania, reguły zysków i strat czy wymiany pieniędzy. Najsłynniejsze stało się zadanie o królikach. Oto ono: „Ile par królików będziemy mieli na końcu roku, jeśli zaczniemy w styczniu z jedną parą królików, ta w każdym następnym miesiącu, poczynając od marca, wyda na świat kolejną parę królików i z każdej pary urodzą się kolejne pary po dwóch miesiącach od narodzin?”. Okazało się, że łączna liczba królików w poszczególnych miesiącach tworzyła zadziwiający ciąg liczb 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. W grudniu będą 144 pary królików. Od trzeciego wyrazu ciągu każdy kolejny wyraz jest sumą dwóch poprzednich. Taki ciąg można tworzyć w nieskończoność. Obserwując przyrodę, można zauważyć, że ciąg Fibonacciego jest wszechobecny. Kwiaty mają liczbę płatków, która jest liczbą Fibonacciego, np. lilia — 1, wilczomlecz — 2, irysy — 3, jaskier — 5, ostróżka — 8, nagietek — 13, stokrotki — 21 lub 34. Cały rozwój rośliny — liczba kolejnych pędów czy gałęzi drzew — tworzy również ciąg Fibonacciego. To dlatego tak trudno znaleźć czterolistną koniczynę, bo liczba 4 nie jest liczbą tego ciągu. Przykłady ciągu Fibonacciego występują, od anatomii człowieka poczynając, a na kształcie galaktyk kończąc. Własności tego ciągu wykorzystuje się w ekonomii, ale również w muzyce, czego przykładem jest kanon D-dur Johanna Pachelbela. To nie koniec magii ciągu Fibonacciego. Jeżeli będziemy dzielić kolejne liczby tego ciągu przez wyrazy poprzedzające, to kolejne wyniki będą coraz bardziej zbliżone do złotej liczby, zwanej też złotą lub boską proporcją. Najczęściej oznacza się tę liczbę literą ϕ, a jej wartość to w przybliżeniu 1,618. Starożytni Grecy uważali złoty podział za idealną proporcję, którą chętnie wykorzystywali w architekturze czy w malarstwie. Złotą proporcję odnajdziemy też w słynnych obrazach Leonarda da Vinci — Mona Lisa czy Ostatnia Wieczerza.Galileusz powiedział, że „matematyka jest alfabetem, za pomocą którego Bóg opisał wszechświat”. A może tajemnice ciągów liczbowych to matematyczne ślady Stwórcy?
|



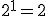 ,
, 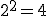 ,
, 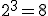 , …,
, …, 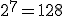 … . Obliczmy:
… . Obliczmy: 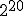 =1 048 576, czyli 104857,6 mm, zatem ponad 104 metry! Niewiarygodne! Ale spróbujmy składać dalej. Przy 42 złożeniu otrzymamy
=1 048 576, czyli 104857,6 mm, zatem ponad 104 metry! Niewiarygodne! Ale spróbujmy składać dalej. Przy 42 złożeniu otrzymamy 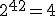 398 046 511 104, czyli ok. 439 804 kilometrów, co jest długością większą niż odległość między Ziemią a Księżycem. Oczywiście takie rozważania są już czysto teoretyczne.
398 046 511 104, czyli ok. 439 804 kilometrów, co jest długością większą niż odległość między Ziemią a Księżycem. Oczywiście takie rozważania są już czysto teoretyczne.