Materiały » Zadania
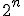- 2. Liczby pseudopierwsze mogą być również pierwszymi. Wtedy skrzat nie uważa już tej liczby za pierwszą. Skosztowanie liczby pseudopierwszej przez Mroczusia spowodowałoby nagły atak trygonometrycznych konwulsji. Liczby te również nie zmieniają koloru na pomarańczowy, nawet po dotknięciu przez tysiące stworków. Niesforny skrzat wkradł się na wieżę z zegarem. Po tej wizycie liczby godzinowe uległy pewnym zmianom i można teraz stwierdzić, że:
Pokaż rozwiązanie »
TWOJE ODPOWIEDZI ZAZNACZONE SĄ KOLOREM FIOLETOWYM
ZADANIE 1 z 1 [#586]
Zadanie 586
W Kwadratolandii można spotkać małe skrzaty Mroczusie. Żywią się one tylko liczbami pierwszymi, inne liczby po ich dotknięciu przyjmują kolor pomarańczowy. Jeśli widzą liczbę, to nie mogą powstrzymać się, by nie spowodować jakieś jej zmiany. Wyjątkiem są jednak liczby pseudopierwsze, czyli postaci n|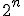 - 2. Liczby pseudopierwsze mogą być również pierwszymi. Wtedy skrzat nie uważa już tej liczby za pierwszą. Skosztowanie liczby pseudopierwszej przez Mroczusia spowodowałoby nagły atak trygonometrycznych konwulsji. Liczby te również nie zmieniają koloru na pomarańczowy, nawet po dotknięciu przez tysiące stworków. Niesforny skrzat wkradł się na wieżę z zegarem. Po tej wizycie liczby godzinowe uległy pewnym zmianom i można teraz stwierdzić, że:
Pokaż rozwiązanie »
TWOJE ODPOWIEDZI ZAZNACZONE SĄ KOLOREM FIOLETOWYM
- ODPOWIEDŹ POPRAWNA
- ODPOWIEDŹ BŁĘDNA
ZADANIE 1 z 1 [#586]